Ackermann steering compensation

A few days ago I posted about problems with the steering linkage introduced by having shock-absorber suspension:

https://bkhome.org/news/202405/trike-steering-cannot-kick-the-can-down-the-road-anymore.html

Another problem is tyre scrubbing when turning a corner. If both front wheels are parallel, when turning a corner, they will be fighting each other. They are following the same radius, whereas the inner one should be following a smaller radius.

This might seem unimportant; however, for a fairly tight corner, say a radius of 2 metres, the scrubbing will be serious. The effect is noticed as tyre squeal and premature wear. I suppose the premature tyre wear is going to happen even for large turning radii.

Ackermann steering geometry corrects for this, causing the inner wheel to follow a smaller radius than the outer wheel. There is a wikipedia page:

https://en.wikipedia.org/wiki/Ackermann_steering_geometry

As I explained in my earlier blog post, I cannot have a tie-rod directly from the steering arms to the wheel-knuckle, as most trikes do. Instead, I have to do it indirectly, as this very rough sketch shows:

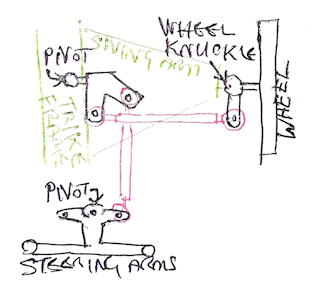
As I pointed out before, exactly how this works will become clearer when photos, even a video, is taken of the contructed trike suspension.

By appropriate geometry, the above design also implements Ackermann compensation. This diagram created in SolvSpace, with dimensions approximately those of my trike, shows both wheels pointing straight ahead:

...the two red lines are the levers attached to the wheel-knuckles. The lines marked as length "298.60" are tie-rods. Notice especially the "52.85" distance between the tie-rod ends.

If the steering arms are turned, so will the front wheels. Those two red lines are the wheel direction. Here is the wheels turned to follow a 2 metre radius:

...those two curves are concentric, that is, the same central point. The inner circle has a smaller radius than the outer. The inside wheel has turned more than the outside wheel, so they are both following concentric circles around the same point. Thus there is no tyre scrubbing.

Notice the "43.70" distance. This shows that the inner wheel has been turned more than the outer. As also shown by the angles of wheels relative to the swing-arms.

Here is the SolveSpace diagram, with a false ".gz" appended to the filename:

https://bkhome.org/news/202405/images/ackermann-5.slvs.gz

The project is moving along; there will be more posts coming soon.    

Tags: light